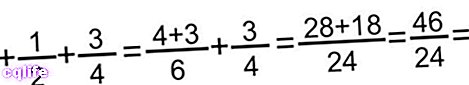نفسر ماهية الإضافة أو الإضافة في الرياضيات وتاريخها وخصائصها وأمثلة. أيضا ، طرق جمع الكسور.

ما هو المبلغ؟
تعتبر الإضافة أو الإضافة عملية حسابية أساسية تتكون من دمج عناصر جديدة في a تعيين عددي ، أي اندماج رقمين للحصول على رقم جديد ، والذي يعبر عن القيمة الإجمالية للرقمين السابقين. الإضافة هي المبدأ الأساسي الذي نتعلم من خلاله الاتصال بالأرقام ، لأن مجرد حقيقة العد واحدًا تلو الآخر (1 ، 2 ، 3 ، 4 ...) تتضمن إضافة 1 (1 + 0 ، 1 + 1 ، 1 + 2 ، 1 + 3 ...).
المجموع عبارة عن عملية حسابية من النوع الذي يسمح بدمج أعداد من الأنواع المختلفة: طبيعي >> صفة, أعداد صحيحة، الكسور ، الحقيقية ، المنطقية ، غير المنطقية والمعقدة ، وكذلك الهياكل المرتبطة بها ، مثل فضاءات المتجهات أو المصفوفات. في الجبر يتم تمثيل الحداثة بالرمز + ، المدرج بين العناصر المراد إضافتها ، ويتم التعبير عنه شفهيًا كـ "more": "1 + 1 = 2" يُقرأ "واحد زائد واحد يساوي اثنين".
من ناحية أخرى ، تُعرف العناصر المراد إضافتها باسم "الإضافات" ، ويسمى الرقم الذي تم الحصول عليه في النهاية "النتيجة".
تاريخ المجموع
تعتبر عملية الجمع من أقدم العمليات الحسابية المعروفة وأهمها. من المعتقد أن كائن بشري منذ العصر الحجري الحديث ، تعاملت بالفعل مع المبادئ الرياضية الأولية ، من بينها الجمع والطرح بالضرورة ، لأن هذه العمليات من السهل إثباتها في مواجهة الإمدادات الزراعية التي زادت وانخفضت وفقًا للوقت من العام.
ومع ذلك ، فإن دراسة الجمع وتطبيقه على كل من الأعداد الطبيعية والكسرية بدأت مع قدماء المصريين ، واستمرت في التطور بطرق أكثر تعقيدًا مع البابليين ، وخاصة مع الصينيين والهندوس ، الذين كانوا أول من جمع الأعداد. . ولكن فقط في عصر النهضة لقد فرضت الطفرة المصرفية مجموع الكسور العشرية واللوغاريتمات المبتذلة.
خصائص المجموع
الإضافة كعملية رياضية لها مجموعة من الخصائص ، وهي:
- خاصية التبديل. يثبت أن ترتيب الإضافات لا يغير النتيجة ، أي أن أ + ب هو نفسه تمامًا ب + أ ، وفي كلتا الحالتين يتم الحصول على نفس النتيجة.
- ملكية مشتركة. يثبت أنه عند إضافة ثلاثة عناصر أو أكثر ، من الممكن تجميع اثنين منهم لحلها أولاً ، بغض النظر عن ماهيتها ، دون تغيير النتيجة النهائية. بمعنى ، إذا أردنا إضافة أ + ب + ج ، فيمكننا اختيار طريقتين: (أ + ب) + ج أو أ + (ب + ج) ، دون التأثير على النتيجة على الإطلاق.
- خاصية الهوية. يثبت أن الصفر عنصر محايد في العملية ، لذا فإن إضافته بأي رقم آخر سيؤدي دائمًا إلى نفس الرقم الأخير: a + 0 = a.
- خاصية الإغلاق. يثبت أن نتيجة المجموع ستنتمي دائمًا إلى نفس المجموعة العددية من الإضافات ، طالما أن هذه بدورها تشترك في نفس المجموعة. بمعنى ، إذا كانت الإضافتان a و b تنتمي إلى N (طبيعي) أو Z (أعداد صحيحة) أو Q (غير منطقي) أو R (حقيقي) أو C (معقد) ، فإن نتيجة المجموع ستنتمي أيضًا إلى نفس المجموعة.
أمثلة على الإضافة
فيما يلي بعض أمثلة الإضافة البسيطة:
- امرأة لديها أربع أزهار ، ولكن اليوم هو عيد ميلادها ، وقد حصلت على ثمانية أزهار أخرى. كم زهرة لديه في نهاية اليوم؟ 4 زهور + 8 زهور = 12 زهرة.
- لدى الراعي 15 خروفًا ، بينما يمتلك زميله 13. إذا قرروا دمج قطعانهم ، فكم عدد الخروف الذي سيكون لديهم في المجموع؟ 15 شاة + 13 شاة = 28 شاة.
- تعطي شجرة التفاح لصاحبها 5 تفاحات في الشهر. كم عدد التفاح الذي سيحصل عليه في نهاية عام واحد؟ بما أن السنة هي 12 شهرًا ، يجب أن نضيف 5 اثني عشر مرة ، مع تطبيق الخاصية الترابطية: (5 + 5) + (5 + 5) + (5 + 5) + (5 + 5) + (5 + 5) + ( 5 + 5) = (10 + 10) + (10 + 10) + (10 + 10) = 20 + 20 + 20 = 60 تفاحة في السنة.
مجموع الكسور
عند جمع الكسور ، هناك اختلاف طرق يمكننا التقدم للحصول على النتيجة ، اعتمادًا على ما إذا كانت الكسور صحيحة وغير صحيحة ومختلطة.
- طريقة جمع الكسور ذات المقام نفسه. هذه أبسط حالة ، حيث نجمع البسط ببساطة ونحتفظ بنفس المقام. فمثلا:
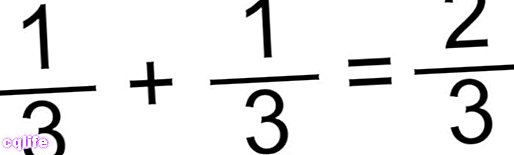
أو
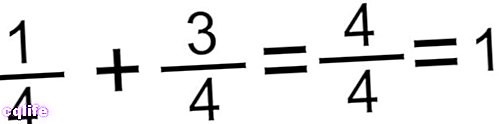
- طريقة الفراشة. تسمح لنا هذه الطريقة بإضافة أي نوع من الكسور ذات المقامات المختلفة ، ببساطة عن طريق ضرب البسط الأول في مقام الثاني والعكس صحيح ، ثم إضافة حاصل الضرب (للحصول على البسط) ، ثم ضرب القواسم للحصول على مقام الكسر الأخير. بمجرد تنفيذ هذه العمليات ، غالبًا ما يتعين علينا تقليل النتيجة. فمثلا:
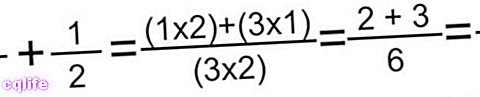
- طريقة جمع ثلاثة كسور. في هذه الحالة ، نضيف ببساطة الأولين ونضيف الأخير إلى النتيجة ، مع تطبيق الطريقة السابقة وتقليل النتيجة أو تبسيطها إذا لزم الأمر. فمثلا: